FIRST ORDER CHEMICAL REACTIONS
Reactions in which rate of reaction is directly proportional to the concentration of the reactant and its power raised to the value of one. Therefore, rate of first order reaction is linearly dependent on the concentration of the reactant. All the radioactive decays comes under first order chemical kinetics.
Let us consider simple reaction in which one mole of reactant decomposed to give product P (R → P)and its rate expression can be expressed as: Rate = k[R]. Let the initial concentration of reactant (concentration of reactant at the start of the reaction (Time = 0)) is [R]0 and the concentration of reactant after time ’t’ is [R]t. As the time progresses concentration of reactant decreases and the concentration of product increases. Therefore, [R]t < [R]0.
Examples to first order reaction
- Decomposition of H2O2
-
All radioactive decays follows first order kinetics
-
Decomposition of N2O5(g)
Integrated rate equation
Let us consider the reaction: R → P, initial concentration of R is [R]0 (or ‘a’ mol/lit) and the concentration of R reduces to [R]t after some time ’t’, where [R]t = [R]0 – x = (a-x) mol/lit. The differential equation and the integrates rate equation is derived as shown below.
Differentail equation is:
\(-\dfrac{d[R]}{dt} = k[R] \quad \Rightarrow -\dfrac{1}{[R]}d[R] = k\,dt\)
\(\text{Integrate both sides with the limits}\)
\(-\int\limits_{[R]_0}^{[R]_t}\dfrac{d[R]}{[R]}= k\,\int\limits_0^tdt\quad {\color{red}\Rightarrow}\quad -(ln\,[R])_{[R]_0}^{[R]_t}= k(t)_0^t\)
\(-(\ln\, [R]_t-\ln\, [R]_0) = k(t-0) \quad {\color{red}\Rightarrow}\quad \ln\, [R]_0-\ln\,[R]_t = kt………(1)\)
\(\ln\, \dfrac{[R]_0}{[R]_t}= kt \quad {\color{red}\Rightarrow}\quad 2.303\, \log\, \dfrac{[R]_0}{[R]_t} = k\,t \)
\({\color{red}{k = \dfrac{2.303}{t}\, \log\,\dfrac{[R]_0}{[R]_t}}}\)
Variation of reactant concentration with time:
Half-life time is defined as the time at which the concentration of reactant is reduced to half of the initial concentration.
As per the definition of half-life time, at time \(t = t_{\frac{1}{2}}\), then concentration of reactant, \([R]_t = \dfrac{[R]_0}{2}\). Substitute these values in the rate constant equation, \(k = \dfrac{2.303}{t}\, \log\, \dfrac{[R]_0}{[R]_t}\)
\(k= \dfrac{2.303}{t_{\frac{1}{2}}}\, \log\, \dfrac{[R]_0}{\frac{[R]_0}{2}} \quad \Rightarrow \quad t_{\frac{1}{2}} = \dfrac{2.303 \times \log\, 2}{k} \Rightarrow t_{\frac{1}{2}} = \dfrac{2.303 \times 0.301}{k} = \dfrac{0.693}{k} \)
Half-life of a first order reaction is: \(\color{red}{t_{\frac{1}{2}} = \dfrac{0.693}{k}}\), therefore the half-life of a first order reaction is independent on the initial concentration of the reactant.
FIRST ORDER GRAPHS-1
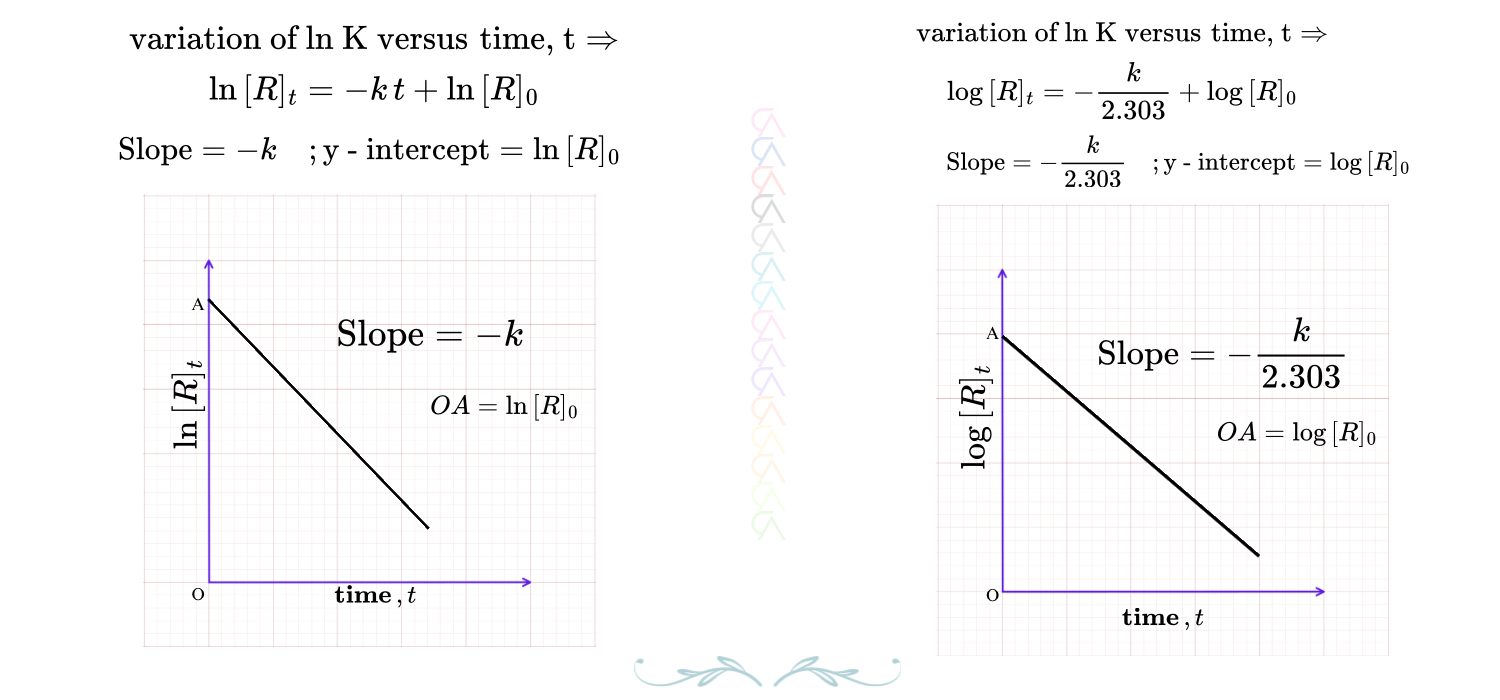
FIRST ORDER GRAPHS - 2

To practice numerical on first order chemical kinetics, remember the following points:
- \(t_{x\%} \Rightarrow \) consider \([R]_0\) as 100 and \([R]_t\) as \(100 – x\). For example: Let time required to complete \(25 \%\) of reaction is represented by \(t_{25\%}\), then take \([R]_0\) as 100 and \([R]_t\) as \(100 – 25 = 75\) and substitute in the first order rate constant equation.
- \(t_f\), where ‘f’ is the fraction of reaction completed, then consider \([R]_0\) as 1 and \([R]_t\) as \(1 – f\). For example: Let time required to complete \(\frac{1}{4}^{th}\) of reaction is represented by \(t_{\frac{1}{4}}\), then take \([R]_0\) as 1 and \([R]_t\) as \(1 – \frac{1}{4} = \frac{3}{4}\) and substitute in the first order rate constant equation.
SOLVED EXAMPLES:
1.Show that for a first order reaction t75% = 2 x t50%.
Solution: Given that \(t_{75\%} \Rightarrow \, [R]_0 = 100\,\, [R]_t = 100-75 = 25\)
\(t_{50\%} \Rightarrow \, [R]_0 = 100\,\, [R]_t = 100-50 = 50\)
From the first order rate constant: \(k = \frac{2.303}{t}\,\log\, \dfrac{[R]_0}{[R]_t}\)
Substitute corresponding \(t_{75\%},\, [R]_0,\, \text{and}\, [R]_t\) values
\(k = \dfrac{2.303}{t_{75\%}}\, \log\, \dfrac{100}{25} \Rightarrow \, k = \dfrac{2.303}{t_{75\%}}\, \log\, 4\)
\(k = \dfrac{2.303\times 2\times \log\, 2}{t_{75\%}}\)………(1)
Substitute corresponding \(t_{50\%},\, [R]_0,\, \text{and}\, [R]_t\) values
\(k = \dfrac{2.303}{t_{50\%}}\, \log\, \dfrac{100}{50} \Rightarrow \, k = \dfrac{2.303\times \, \log\, 2}{t_{50\%}}\) …….(2)
equate equations (1) and (2)
\(\dfrac{2.303\times 2\times \log\, 2}{t_{75\%}} = \dfrac{2.303\times \, \log\, 2}{t_{50\%}} \)
\(\therefore \, t_{75\%} = 2 \times t_{50\%}\)
2.If a first order reaction takes 30 minutes to complete 30% of the reaction then what is the half life of reaction.
Given: \(t_{30\%} = 30\) minutes and \(t_{\frac{1}{2}}\) = ?
First order rate constant: \(k = \frac{2.303}{t}\,\log\, \dfrac{[R]_0}{[R]_t}\)
\(t_{30\%} \Rightarrow \, [R]_0 = 100\,\, [R]_t = 100-30 = 70\)
\(\Rightarrow k = \frac{2.303}{t_{30\%}}\,\log\, \dfrac{100}{70}\Rightarrow k = \frac{2.303 \times (\log\,10 – \log\, 7)}{30 \text{min.}}\)
\(\Rightarrow k = \frac{2.303 \times (1 – 0.8451)}{30 \text{min.}} = \frac{0.3567}{30}\Rightarrow k = 1.19 \times 10^{-2} \text{min}^{-1}\)
\(t_{\frac{1}{2}} = \dfrac{0.693}{k} \Rightarrow t_{\frac{1}{2}} = \dfrac{0.693}{1.19 \times 10^{-2}} = 58.23\) minutes.
3.In a first order reaction reactant takes 100 minutes to reduce its concentration to 1/5th of its initial concentration. What is the half-life time of reaction?[Given: log5 =0.699]
Given: t = 100 minutes, \([R]_t = \frac{[R]_0}{5};\quad t_{\frac{1}{2}} = ?\)
From first order rate constant: \(k = \dfrac{2.303}{t}\, \log\, \dfrac{[R]_0}{[R]_t} = \dfrac{2.303}{100\text{min}}\, \log\,\dfrac{[R]_0}{\dfrac{[R]_0}{5}}\)
\(k = \dfrac{2.303 \times \log\, 5}{100} = 2.303 \times 10^{-2}\times 0.7 = 1.61 \times 10^{-2}\, \text{min}^{-1}\)
\(t_{\frac{1}{2}} = \dfrac{0.693}{k} = \dfrac{0.693}{1.61 \times 10^{-2}}\, \text{min}\)
Half -life time = 43 minutes
4.If half-life time of a first order reaction is 100 minutes then how much time it takes to reduce its concentration to 1/10th of its initial value?
Given: \(t_{\frac{1}{2}} = 100 \text{min.}; \quad [R]_t = \frac{[R]_0}{10}; \quad t = ?\)
We know that: \(k = \dfrac{2.303 \times 0.301}{t_{\frac{1}{2}}}\) and \(k = \frac{2.303}{t}\, \log\, \frac{[R]_0}{[R]_t}\)
Equate Both the rate constant formulae and substitute the values
\(\dfrac{2.303 \times 0.301}{100\, \text{min.}} = \dfrac{2.303}{t}\, \log\, \dfrac{[R]_0}{\frac{[R]_0}{10}}\)
\(t = \dfrac{100 \times \log\,10\, \text{minutes} }{0.301} = 332.2\) minutes