ARRHENIUS EQUATION
Rate of reaction depends on the temperature. In general the rate of reaction increases as the temperature increases. Arrhenius gave a mathematical relation of variation of rate constant with absolute temperature. In theoretical explanation of rate of reaction dependence on temperature involves the collision of molecules. As the temperature increases velocity of molecules increases, which increases their average kinetic energy. Therefore, the fraction of molecules which are having kinetic energy enough to cross the activation energy barrier increases, therefore rate of reaction also increases.
Reactants already has some energy, and the collisions among the reactants in a proper orientation leads to form an activated complex, which has maximum energy. The resulting activated complex may breakdown to form products or to form reactants back. Minimum energy required by the reactants to form the activated complex is known as activation energy, Ea. Rate of reaction depends on the activation energy as well as absolute temperature. Reactions which are having low activation energy proceeds with faster rate.
Mathematical expression
Mathematically, Arrhenius gave a relationship between rate constant, k and activation energy, Ea and absolute temperature.
\(k = A\,\, e^{-\dfrac{E_a}{RT}}…….(i)\)
k = Rate constant
Ea = Activation energy
A = Pre-exponential factor or Arrhenius constant or frequency factor
T = Absolute temperature
R = Universal gas constant (R = 8.314 J mol-1K-1)
The fraction $e^{\dfrac{-E_a}{RT}}$ is the fraction of molecules which are having kinetic energy more than or equal to the activation energy. Units of activation energy are J mol-1 or Cal mol-1.Increase in temperature or decrease in activation energy by adding a catalyst increases the rate constant value. Activation energy can be calculated by measuring two rate constants at two different temperatures. Units of pre-exponential factor are same as that of order of reaction. For example units of A for a first order chemical reaction are s-1.
From Arrhenius equation (i)
\(k = A\,\, e^{-\dfrac{-E_a}{RT}}\)
Take ‘log’ on both sides
\(\ln\,k = \ln(A\, \, e^{\dfrac{-E_a}{RT}}) \Rightarrow \ln\,k = \ln\,A + \ln\,(e^{\dfrac{-E_a}{RT}})\)
\(\ln\, k = \ln\,A – \dfrac{E_a}{RT}\, \ln\,e \Rightarrow \color{red}{\ln\, k = \ln\, A -\dfrac{E_a}{R}\, \dfrac{1}{T}}……(ii)\,\, (\because \ln\, e =1)\)
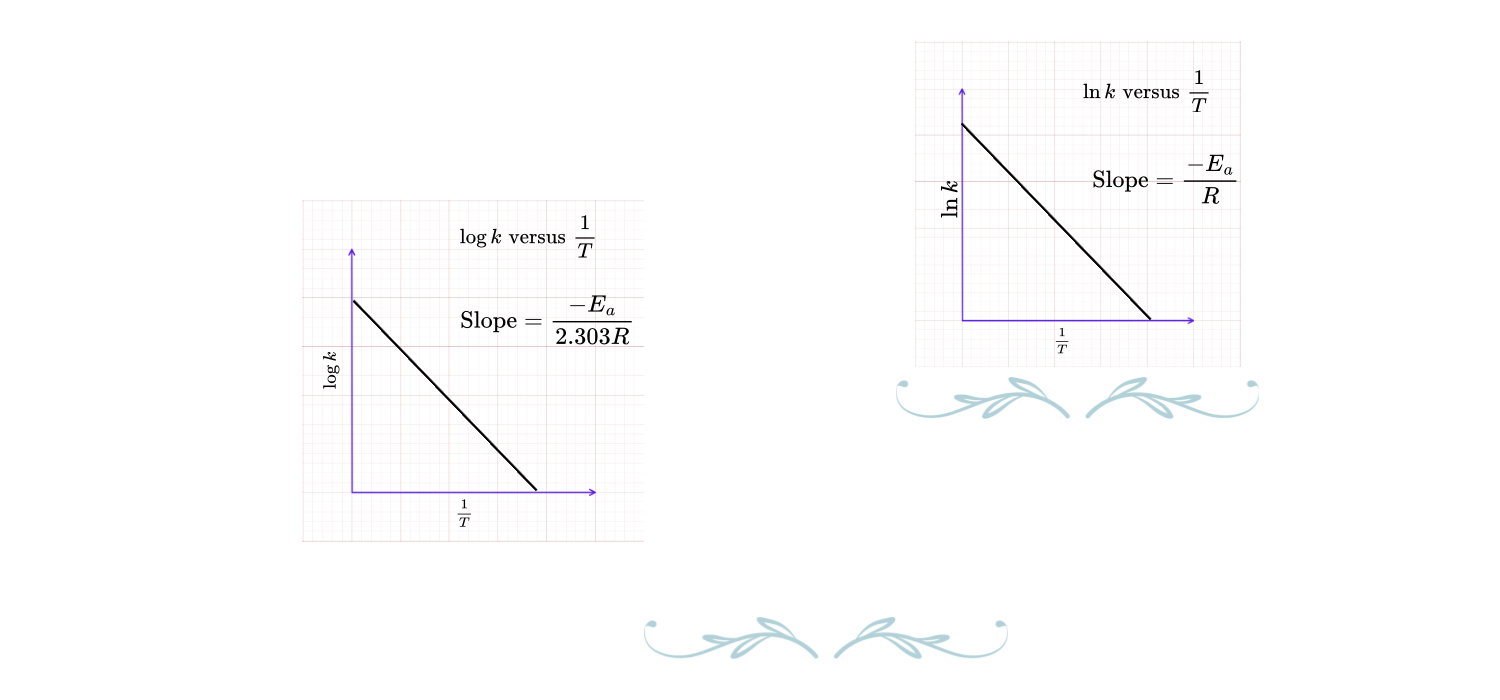
Equation (ii) is $y = mx + C$ format and graph of $\ln\,k$(y-axis) versus $\frac{1}{T}$ is a straight line with negative slope ($\frac{-E_a}{R}$) and y – intercept $\ln\, A$.
\(2.303\,\log\,k = 2.303\,\log\,A – \dfrac{E_a}{R}\,\dfrac{1}{T} \Rightarrow \color{red}{\log\,k = \log\,A-\dfrac{E_a}{2.303R}\,\dfrac{1}{T}}….(iii)\)
Equation (iii) is $y = mx + C$ format and graph of $\log\,k$(y-axis) versus $\frac{1}{T}$ is a straight line with negative slope ($\frac{-E_a}{2.303R}$) and y – intercept $\log\, A$.
Differentiation of lnk with T
\(k = A \, e^{\dfrac{-E_a}{RT}}\)
Take ‘ln’ both sides
\(\ln\, k = \ln\, A + \ln \, (A\,e^{\dfrac{-E_a}{RT}}) \Rightarrow \,\,\ln\, k = \ln\, A -\dfrac{E_a}{RT}\quad (\because \ln\,e^x = x)\)
Differentiate this equation with respect to ‘T’
\(\dfrac{d(lnk)}{dT} = \dfrac{d(lnA)}{dT} -\dfrac{E_a}{R}\, \dfrac{d}{dT}\left(\dfrac{1}{T}\right)\)
\(\dfrac{d(lnk)}{dT} = \dfrac{E_a}{RT^2}\)
\(\dfrac{d(lnk)}{dT} = \dfrac{E_a}{RT^2}\)
Integrate both sides with the limits ($k_1$ is at $T_1$ and $k_2$ is at $T_2$)
\(\displaystyle \int\limits_{k_1}^{k_2} \dfrac{d(ln\,k)}{dT} = \displaystyle \int\limits_{T_1}^{T_2} \dfrac{E_a}{RT^2}\)
\(\{ln\,k\}_{k_1}^{k_2} = \dfrac{E_a}{R}\, \left\{ \dfrac{-1}{T} \right\}_{T_1}^{T_2}\Rightarrow (\ln\,k_2 – \ln\,k_1) = \left(\dfrac{-1}{T_2}- \dfrac{-1}{T_1}\right)\)
\(\ln\,\dfrac{k_2}{k_1} = \dfrac{E_a}{R} \left(\dfrac{1}{T_1}-\dfrac{1}{T_2}\right)\)
\(\log\,\dfrac{k_2}{k_1} = \dfrac{E_a}{2.303R} \left(\dfrac{1}{T_1}-\dfrac{1}{T_2}\right)\)